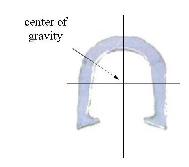
ALL OTHER LINES THROUGH THE CENTER POINT WILL EVENLY DIVIDE THE BALANCE OF THE WEIGHT OF THE SHOE ON EITHER SIDE OF THE LINES
9B  If this proposition does not interest the reader, this section may be skipped and move down to section 10 and read on.  To test if the center point has been found, stretch a piece of Scotch tape across the center line (wrap it around a time or two to make it stronger) connecting the blades and mark a black dot where the center line that divides the horseshoe symmetrically down the middle crosses this line.  Now placing the tip of your index finger under this dot, see if the shoe remains balanced while holding it up.  WARNING:  Don't hold it very high up off the ground over a bare foot before attempting to hold it up this way unless you are very certain that you found the center.  Again I state "all other lines drawn through this center point will evenly divide the balance of the weight of the shoe on either side of the lines."
But what about the lines drawn in this next picture to the left--line A going through the center point and especially line B?  How can the horseshoe still be balanced when there is obviously more weight on one side of the line than on the other side of the line?  With the line A division, without cutting the shoe up with a hacksaw, it might be argued that the weight of the portion of the shoe given up from the left half of the shoe to the right half of the shoe in the upper left of our pictured shoe between the vertical line Y and line A is the same weight as the portion of the heavier right heel calk, with the point, given up from the right half to the left half of line A.  But the line B division leaves no such argument.  Line B has the left half of the shoe gaining the metal between line Y and line B in the upper right of our pictured shoe and giving up empty air between line Y and line B in the lower left of our pictured shoe.  How can this empty air be the same weight as a piece of metal?  Why wouldn't our shoe be unbalanced with more weight on one side of the shoe than on the other side?  This apparent problem in physics will be answered later on in this writing in section 20B.  Just think about it for a while.  (Hint:  a famous Greek geometrician and philosopher named Archimedes once proclaimed, "Give me a place to stand and with a lever I will move the whole world."  Living in a period from 287 to 212 BC, this man discovered principles of the lever and of specific gravity which answers what seems to be a paradox of unequal weights on two sides of a "see-saw" remaining in a state of balance.)

10  IMPORTANCE OF KNOWING WHERE THE CENTER OF GRAVITY IS
11  THROWING AN OPEN SHOE AT THE STAKE DOES NOT HAVE TO DEPEND ON LUCK
12  BACK SWINGS MAY VARY
13  STRAIGHT BACK SWING AND FORWARD SWING
14  HOW MUCH TURN ROTATION TO PUT ON A SHOE
14B  EFFECT OF THE STEP ON THE FORWARD MOTION OF THE SHOE
15A  HOW MUCH TURN FOR HOW LONG
15B  WHAT AMOUNT OF INFLUENCE STAYS WITH THE SHOE INTO FLIGHT?
15C  . . . AND THE IMPORTANCE OF THE FOLLOW THROUGH
16  FACTOR OF WHERE SHOE IS GRIPPED
17  SHOE CAN WORK ITSELF OR TURN ITSELF

WHAT IS A WOBBLE IN A SHOE (PART 1)
18A  What is a wobble in a shoe and how can it be eliminated?  Some might refer to a wobble shoe as when the horseshoe is released in such a position that one half of the shoe, open end points are up versus closed end down (or vice versa) or gripped blade points up versus the loose blade down (or vice versa) or some blend of these halves of the shoe around the center of gravity, is higher or lower than the other half.  With this definition of a wobble in the shoe, only a shoe that is thrown perfectly level with all parts of the shoe perfectly parallel to the ground during flight would not be considered a wobble shoe.  Others would say these are not wobble shoes, but these are simply shoes thrown with the points or heel calks up (or down); or the gripped point up (or down). Some may even believe a true wobble in the horseshoe is caused by throwing a shoe that has the turn rotation motion applied at a point close to the center of gravity of the shoe, but not quite in the center.  (Read through this line of thought, before reading the following section 18B, showing the error of this way of thinking).  They would contend that if that turn rotation center is a half inch from the true center of the shoe, then the shoe will wobble its turn center toward the true center and continue wobbling unbalanced until it reaches a balanced spin, if it can before reaching the landing point.  If it was turned around a center that is an inch or more from the true center, then it may never reach a balanced state during flight before landing and may land unbalanced.  A balanced thrown shoe can be spotted a mile away.  And remember, no matter what point the rotation turn influence is pivoted around, the center of the shoe or off center, it is the place at the end of the court that the center of the shoe is thrown at that will be hit.  The off center wobbling shoe may even hit the stake as a ringer, if the center of the shoe was thrown at the stake in a straight line, far enough and if it happened to be open when it got there.  But the off center shoe will not have a pretty flight.  It would be their opinion it will be the shoe that seems to have a lot of wobble.  Therefore it would be their belief that many horseshoe pitchers do have some wobble in their shoe because they are not turning the shoe around the true center of gravity of the shoe.  Note:  I expressed the above, because when I first started writing this page, I believed all of this about a shoe spinning around an off center point in the shoe.  I corrected my own thinking in section 18B below.

WHAT IS A WOBBLE IN A SHOE (PART 2)
18B  In 15B above, earlier in this writing, I stated that "the exact rate of turn on the shoe at the very moment of release, which is the only moment of influence which really influences the shoe".  Then in discussing the different theories in what constitutes a "wobble shoe" (in 18A above), this principle was ignored.  In other words:  No matter where the off-center point is that a pitcher might be applying turning motion around; (1)the center of the shoe will be the portion of the shoe that heads straight down the court in the exact direction it was thrown and, (2) only the last motion "in relation" to the actual center of the shoe will influence the shoe around that center--even though the pitcher might have consistently applied a nice smooth turn motion around an off-center point.  Its like saying the shoe knows where its center is, even if the pitcher does not.  So whatever off-center point the pitcher is trying to revolve around and influence, it is actually the true center of the shoe that will receive the effective influence on it at the point of release!
 

 

The Theory of Shoe Tilt Introduction:  The following sections on shoe tilt are very speculative.  Although in my mind, I can picture a horseshoe spinning only in a particular angle plane (or tilt) all the way down to the other stake; in practice, I don't know that anyone would exert the type of force on the shoe that would cause this to occur.  So these sections are more for speculation and theoretical thinking.  Some benefit may be realized by thinking about the theory of shoe tilt (especially in section 18C in the discussion on improper lift throwing off the alignment of the horseshoe). I do not deny that there is a tilt when the shoe is released.  I'm just not sure in practice that any pitcher would spin the shoe to maintain a particular "path tilt" angle.  In practice, horseshoes seem to tumble with the shoe spinning in the position the shoe was in at the point of release (i.e. both heel calks up, one particular heel calk up and the other down, both heel calks down, etc.).  Turning shoes tend to have a predominant amount of horizontal motion in the turn as opposed to vertical motion (or more motion in the angle of the upward path of the shoe) that conforms with gravitational pull versus vertical lift beyond the upward path of the flight of the horseshoe.  As discussed elsewhere on this page, too much vertical lift in relation to the upward path of the shoe will cause the shoe to flip or turn over. I originally did not have these sections on shoe tilt highlighted with "yellow" colored background and did not have the introduction above preceding the sections.  After receiving an email from someone saying they did not follow exactly what I was trying to say concerning shoe tilt, I thought some more about it and realized that much of what I was thinking and writing about on shoe tilt was not that practical, but nonetheless interesting from a theoretical standpoint.  Again, I emphasize that I'm not trying to sound like a know-it-all, I'm just expressing thoughts that are going on in my mind when I think on these things.  I think the physics of horseshoe pitching is fascinating and very interesting to think about. SHOE TILT AND SHOE LIFT (THE UPWARD PATH) 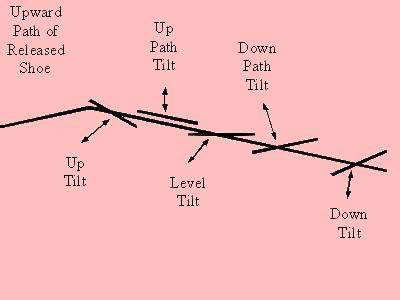18C  The tilt of a shoe is the relationship of the plane the shoe is spinning in, at the point of release, to the upward path of the shoe in flight.  This pink chart of the “Upward Path of the Released Shoe” shows the upward path of the shoe with five tilts shown:  Up Tilt, Up Path Tilt, Level Tilt, Down Path Tilt, and Down Tilt.   On the other hand, lift is the influence put around the center of gravity of the shoe during the upward portion of the forward swing and actually the lift force on a side of the shoe at the point of release.  Any turning motion put on the shoe outside of the plane that the shoe is in is considered lift.  A shoe that is delivered as a level to the ground dinner plate is having a back lift applied to the shoe to keep it level right up to the point of release.  In order for the center of gravity of the shoe to stay on the straight path to the stake, any lift applied in the front, back or the side of the shoe must have a corresponding and equal “drop” to the opposite side of the shoe.  Putting a side lift on a shoe without a corresponding and equal drop on the opposite side of the shoe through the center of gravity of the shoe will cause the center to change direction. This would explain why pitchers who put a side lift on a shoe improperly, often find their shoe heading for the right or left side of the stake.  They began on their upward swing with the center of the shoe heading for the stake, but an improperly applied side lift “pulled” the center to the right or left slightly.  Looking at the drawing at the left (viewed from behind the pitcher and looking down court), HS1 (horseshoe #1 position) with the D1 (direction of the center of the shoe to the stake) is thrown off course if the left side of the shoe is lifted (heel calks) with a pivot on the right side of the shoe (toe calk), with HS3 the position of the shoe upon release and D2 is the new direction of the center--to the left of the stake.  If  the toe calk had been dropped as the heel calks were lifted, then HS2 would have been the release position of the shoe beginning at HS1 and the center of HS2 would still be in line with the stake (note:  the right half of the shoe in HS2 moved to the right as the shoe HS1 was lifted to position of HS2, keeping the center on course.)  It doesn't take much visualization to see what would happen in the drawing to the left, if when the shoe is lifted from HS1 to HS3 with the heel calks to the left moving straight forward instead of the toe calk moving straight forward that the center would be pulled to the right for a right handed horseshoe pitcher, thus causing the center of gravity of the shoe to head to the right of  the stake or to the right of direction D1.  All of this is to illustrate that the pitcher must not alter the course of the center of the shoe during any lifts placed on the shoe. All shoes have at least a little lift or drop in the shoe (in relation to the upward path of the thrown horseshoe) except for one particular delivered shoe.  The exception is the shoe that is completely in the delivery plane at the bottom of the swing already in the correct Up Path Tilt position.  The full upswing of the shoe would have to keep the shoe on this delivery path plane with only turn rotation motion placed on the center of the shoe and no lift (in relation to the delivery path) needed on the shoe.  This is what I’ve referred to as a Up Path Tilt shoe.  If the pitcher can hold the shoe at the bottom of the swing and apply only revolution turn motion around the center of gravity of the shoe that is in the delivery plane only, the shoe will travel only in the delivery plane without any lift, thus maintaining its Up Path Tilt.  Even a Level Tilt shoe will need a little lift in back in order to maintain its level position during flight along a delivery path that is slanted up and out.  This is where all of this gets a little confusing. We are discussing Tilt and Lift in relation to the path of the released shoe, not to ground level.  Also, we are discussing the path of the released shoe as a line when we are referring to the center of the shoe traveling on the line and we refer to the path of the released shoe as a plane when we are referring to the whole shoe measuring a maximum of 7-1/4 inches wide and 7-5/8 inches long.  (Note:  If a shoe is thrown with no turn rotation, but only lift, then it is a flip shoe and had better be open upon release if it is to have a chance of going on as a ringer.)  To help visualize the horizontal and vertical plane that heads straight for the stake at release point of the shoe, picture a little 8 inches wide miniature highway going from the release point of the hand heading up and out from the pitcher, coming to a peak high point where the shoe then begins it's descent down towards the stake.  This little 8 inches horizontal highway would end about 4 inches up the stake from the bottom of the pit and the middle of the stake would be dead center in the middle of this little highway. The vertical delivery plane referred to in this writing would be a little 8 inches high wall that would intersect this horizontal highway right down the middle and would end with the bottom of the wall in the pit and the top of the wall 8 inches up the stake.  The delivery path "line" to the stake is where these two planes--the horizontal highway and the vertical wall--intersect.  Most horseshoe pitchers who desire to throw an Up Path Tilt shoe will not be able to have the shoe at the bottom of the forward swing beside the leg in the exact horizontal highway that leads to the stake; therefore, they will have to apply some lift to get the shoe in the Up Path Tilt position at the point of release.  But then the lift in the shoe will cause it to become an Up Tilt shoe before it reaches the high peak of it's flight.  Therefore, if an Up Path Tilt shoe is desired at the high peak of it's flight, the proper lift will need to be applied and something closer to a Level Tilt, Down Path Tilt or a Down Tilt will have to be released with the lift on it to make it an Up Path Tilt shoe sometime during it's flight.  In 18E section below, I explain the wrist motion I use to try to counter or reduce the lift influence on my shoe I want at the peak of it's flight.  Too much lift influence on the shoe and the pitcher will be looking at a vertical leaning shoe at some point in it's flight.  This shoe is discussed in section 19 below. SHOE TILT AND SHOE LIFT (THE DOWNWARD PATH) 18D  The yellow “Downward Path of the Released Shoe” chart shows what all five of the tilts during the “Upward Path of the Released Shoe” look like during the downward path.  I believe the pitcher should strive to throw a shoe tilting between the Up Path Tilt and the Down Path Tilt; and maybe ideally the Level Tilt at the peak high point of the flight of the horseshoe.  I further believe the Up Tilt and Down Tilt shoes (tilting above or below the upward path and the downward path) will be less stable shoes during flight and landing, especially the more degrees they are thrown above the Up Path Tilt or below the Down Path Tilt.  All of this discussion on the tilt and lift on a horseshoe is to impress on the horseshoe pitcher that nothing mysterious begins happening to a horseshoe once it leaves the hand of the pitcher.  All of this discussion is to explain that what is taking place with the shoe during the forward swing and especially from the leg on up to the release of the horseshoe, while it is still in the pitcher's hand, is what determines the type of flight the shoe will have.

SHOE TILT AND SHOE LIFT (MY PERSONAL DELIVERY)
(This section is followed by 18F, where I "disclose" what worked well for me after experimenting all summer long in the year 2005)
18E  With my own personal delivery, at the end of last summer, I worked on delivering a right handed 1-1/4 CW turn shoe from the left walkway, gripping the shoe at the heel calk with the little finger over the inside point.  I passed my leg with about a 45 degrees cocked shoe (halfway between vertical and flat), applying about 1/8 turn rotation motion around the center of gravity and bending my wrist back to apply a back lift and a front drop on the horseshoe to achieve a level tilt at the release point of the shoe.  The wrist will bend about 45 degrees back without discomfort.  I presently believe the 45 degrees or 1/8 lift of the back and drop of the front of the horseshoe by the bending of the wrist neutralizes the 1/8 or 45 degrees lift of the front while applying the 1/8 turn rotation motion around the center of gravity of the shoe.  If I find this delivery to be too stressful over time on my wrist bending back 45 degrees, I will experiment with having my wrist bend 45 degrees inward (the natural bend) at the bottom of my forward swing.  (Note:  most wrists will bend 90 degrees inward with comfort, so a 45 degrees bend should be less stressful than a back bend of the wrist).  To visualize the position this horseshoe would be in at the bottom of the forward swing; first, picture the shoe vertical beside the leg; second, apply a 45 degrees clockwise turn of the heel calks (90 degrees CW turn of the heel calks would make the shoe flat beside the leg, pointing the heel calks at the leg—with no rotation turn potential on the shoe for a pure 1-1/4 CW delivery).  45 degrees or 1/8 cocked position leaves a potential 1/8 turn or 45 degrees turn in the approximate 4 feet of upward and out swing.  Third, visualize bending the wrist 45 degrees inward, which raises the loose heel calk by 45 degrees.  During the 4 feet upswing of the delivery, the wrist slowly straightens out and is completely lining up with the arm at the point of release of the horseshoe for a level tilt delivery.  I may not be able to do this physically or consistently, but I’ll give it a try next summer.  At this point, some horseshoe pitchers would say that the wrist should never bend when delivering a turn shoe, but stay in a fixed position as an extension of the rest of the arm.  They would emphasize that the natural turn of the arm with the underneath of the wrist facing the leg (or cocked 45 degrees beside the leg) and then the underneath of the wrist pointing up upon release of the shoe (or cocked 45 degrees upon release of the shoe) is what puts the natural 1/8 to 1/4 turn on the shoe.  These pitchers do not concern themselves with a little wobble with the shoe in flight.

 

A VERTICAL SHOE
19  All the thrown shoes talked about so far are shoes that are relatively horizontal spinning shoes.  One side of the shoe may be a little higher than the other side while spinning, but the shoe’s center of gravity never has any metal of the shoe close to the top of it as it spins for the stake.  A shoe I think is often mistaken for a wobble shoe because of it’s peculiar appearance while in flight would be a shoe thrown that is closer to spinning vertically than it is to spinning horizontally.  A “perfectly vertical spinning shoe” could be thrown by greeting the stake with the shoe in a perfect vertical position.  In other words, the gripped and loose blade of the shoe would line up exactly up and down with the stake.  The shoe would maintain this vertical position all the way back in the back swing and all the way forward in the forward swing and the turn rotation motion would be easily applied around the center of gravity of the shoe, because that center of gravity would be always running along the line to the stake along with both blades of the shoe.  The problem is that a perfectly thrown pure vertical shoe would hit the stake by both blades of the shoe on the open end points and could not go on.  But it would be a heck of a good alignment throw for practice.  Note:  Since the stake at the other end of the court is vertical, then it would be advisable to throw a shoe that spins closer to a horizontal than to a vertical flight.  Remember, a shoe arriving at the stake in a perfectly horizontal position has 3 and 1/2 inches open between the points to go on the stake; whereas a shoe that is coming in leaning toward vertical cuts that distance to half that or less than half that.

SOMETHING TO THINK ABOUT
20A  A shoe that is released from the hand that is pointing closer to 6 O’clock or 12 O’clock (up or down) than it is to 3 O’clock or 9 O’clock (left or right), as if you were throwing at a face of a clock would be a “vertical leaning” shoe as opposed to the normal “horizontal leaning” shoe.  Put another way, a perfectly thrown horizontal shoe will be perfectly level with zero degrees tilt to the left or right when released.  A vertical leaning shoe will be tilting up or down more than 45 degrees.  The perfectly thrown vertical shoe will be spinning at 90 degrees from the level horizontal position.  Any shoe over 45 degrees during flight will be a vertically leaning shoe.  A shoe with a vertical lean in flight will appear to be very different looking in flight until it lands.  Since most of us are used to watching shoes nearer to zero degrees horizontal, the appearance of a vertical leaning shoe will look different.  Here is a test question:  Is it possible to throw a ¼ turn with a full flip (thrown clockwise or counter clockwise depending on whether the heel calks are pointing to the left or right upon release)?  And if so, what would the shoe look like half way down the court (you may need the assistance of a paper clip bent into a horseshoe shape, with the little hooks created with pliers, to work this out in front of your own eyes and be sure to keep the center of gravity of the shoe in mind while following it’s path).  Also, draw a straight line on a piece of paper and hold your little horseshoe with the center always over this line as you move it down the line and watch your little horseshoe turn.  Try this with a clockwise turn and then with a counter-clockwise turn.  It doesn’t matter if you are right handed or left handed to work it out!  (Here is a hint to the answer of how the shoe will look in the air:  The shoe will have completed half the ¼ turn or 1/8 of a turn and the shoe will have completed half of the flip.)  This might be a nice exercise for the pitcher who currently flips the shoe, but wants to learn to convert to a turn shoe.  The pitcher will still be flipping the shoe one full flip, but also learning to turn the shoe ¼ in order to be open on the stake.

GIVE ME A PLACE TO STAND AND WITH A LEVER I WILL MOVE THE WHOLE WORLD--ARCHIMEDES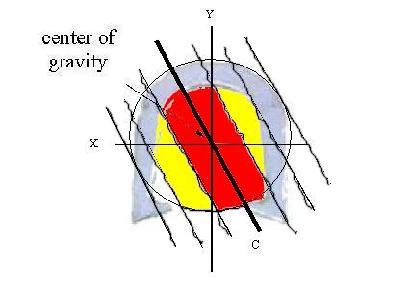
20B  If this proposition does not interest the reader, this section may be skipped and move down to section 21 and read on.  The problem or quandary we posed in 9B was how a shoe can remain in a state of balance when a line through the center point dividing the shoe into two balanced halves may be dividing the shoe into two halves of unequal weight.  The picture to the right shows one such division.  Line C drawn through the center of gravity of the shoe puts more weight onto the right half of the shoe than on the left half (reread 9B above again for more depth into this question).  But what Archimedes showed us over 2000 years ago is that where that weight is placed on each side in relation to the center or the fulcrum is also a factor.  Remember as a kid getting on a see-saw with some kid who weighed more or less than you.  The two of you could get the see-saw perfectly balanced by the heavier one of the two sides moving closer to the center point or fulcrum.  In the shoe pictured to the right with line C dividing it through the center of gravity, even though the right side has more weight, much of the weight on the right side is in the red zone very close to the center line (two portions of metal including the bulk of the heaviest portion--the heel calk), with some more of it in the yellow zone (two more slices of metal).  Only the corner edge of the weight of the right upper part of the shoe is outside these two distance zones I've created here.  Note that even this portion is within the circle drawn around the center of the shoe and within the outside line which is parallel to center line C.  On the left half of the shoe, even though less weight is on this half, only a little of its weight is in the red zone, a little more is in the yellow zone, and the rest of its weight (including the heaviest part of the shoe in the heel calk) farther beyond the yellow zone and beyond the circle around the center of gravity and much of it outside of the line that is parallel to line C that runs through the center of the shoe.  To make a long story short (its probably too late for me to do that now!) the side with more weight has enough of the weight closer to the center of the "see-saw" to keep the two sides in balance.  A shoe thrown that is spinning perfectly around the center of gravity of the shoe would be a perfectly balanced shoe at every stage of it's flight--not just when the Y axis or the X axis is pointing at the stake.

WHEN A TURN SHOE FLIPS
21  Remember that time or two (or three or four, etc.) that you threw your horseshoe and it went on the stake, but it landed upside down from the way you threw it?  (You threw it with the toe calk at the closed end down, but it landed with the toe calk up).  You may have noticed it happen while in the air or you may have been surprised, when you walked down and leaned over to pick it up (I’ve done it and I know I’ve done it when I see it in flight).  This can only happen if the pitcher puts influence on the spin of the shoe that allows some metal on the shoe to pass over or under the center of gravity of the shoe (that is the definition of throwing a flip shoe—think about it).  Now visualize or use your little paper clip horseshoe to view what would take place on a 1 cw or ccw full turn - with one full flip shoe.  Can you create the position of the shoe at half court?  Hint:  If you do it right, the full flip shoe with no turns will be in a perfect horizontal position with both points or the open end of the shoe pointing straight at the pitcher after completing half a flip--assuming it was released with the points or open end of the shoe pointing at the opposite stake at the release of the shoe.  If I did it right, the 1 cw or ccw full turn – with one full flip shoe at half court will be in a perfect vertical position with both points pointing at the pitcher.  Also, a line drawn straight up the stake will go right through the entire horseshoe.  Can a real horseshoe even be thrown this way with enough turn rotation motion along with flip influence to get the shoe to complete this flight?  Just something to think about.  This might also be a good shoe for the flip shoe pitcher to experiment with if wanting to convert over to a turn shoe.  Once they have learned to do this, they can simply eliminate the flip influence on the shoe and add another ¼ turn of rotation or take off ¼ turn of rotation and they are throwing a 1-1/4 turn shoe or a ¾ turn shoe.

PRACTICING HORSESHOES IN THE HOME
22  During the winter months, a pitcher can practice the greeting, back swing, and forward swing of the horseshoe, while applying the turn rotation motion to see if the center of the gravity of the shoe is staying on the imaginary line to the stake, while being confined indoors.  By being in a long room, preferably a hallway, where the pitcher can safely swing the shoe without fear of hitting anyone around who might pop up.  A closed door behind is a good idea, with all the doors immediately around your swinging area also closed, so no one walks out and gets clobbered.  (I would not even suggest anyone do this if they have small children in the home or have any pets who might walk into the back swing and receive a concussion to the head or some other body part).  Take a rope or thick wire and stretch it out straight down the hallway.  Attach it to the end somehow.  This line represents the straight line to the opposite stake the pitcher is swinging at to hit the ringer.  A more elaborate set-up can be constructed, if space allows, where cardboard or wood or some material measuring 18 inches across, so the position of the stake that is beside the pitcher can be marked with half a big black 1” dot.  The material should then be 3 feet long running down the hall representing the other dimension of the fourth of the pit beside the pitcher and the 3 feet leading to the foul line (use the length measurement of the pits you normally pitch at in the better weather).  Now take the end of the rope that is not attached at the pitching end and stretch it across the area where the swing is going to take place.  If you have a mathematician in the house, they can calculate the exact angle the rope or wire needs to go if it were actually stretched 40 feet from the stake dot at the pitcher’s end and where the stake would be at the other end.  Example:  Once it is determined how many inches the rope will lay from the imaginary stake at the pitcher’s end toward the pitcher, say exactly 18 inches towards the edge of the pit plus 2” into your walkway, then have the mathematician figure the angle if the rope went 40 feet or 480 inches (40 X 12”)  480 inches divided by 20 inches equals 24 inches.  In other words for every 2 feet straight down your hall (not straight down the rope), your rope would be one inch away from your straight line down the hall.  (This method of marking the pitching line in relation to the line between the two stakes does not require that you have a mathematician figure the angle).  If you have a hall that is 40 feet or 480 inches, the rope would be 20 inches away from your straight line down your hall, which would attach it to the place where the stake would be anyway.  (Heck, if you have a hall that is 40 feet, just cut the floor out at both ends and put in real pits, tear out the ceiling over the area and pitch real horseshoes in your hallway, arching into the attic, all winter long).

ANGLE OF THE LINE TO THE STAKE
23  If all of this seems confusing, remember, I said if you had a mathematician in the home, have them read this and make it their project to help you out on the angle of the rope down the hall.  If you don’t have one, then just make sure if your hallway is only say 10 feet, then the rope is not more than a fourth of the way (5 inches in) toward what would be the straight line between your two imaginary stakes.  15 feet down the hall would be just short of halfway toward the imaginary line between the stakes (not to be confused with the imaginary line between the pitcher’s swing and the stake being swung at, which is marked with a stretched rope or heavy wire).  Now that the pitcher has the indoor practice court constructed, it is time to try it out.  (Note:  If you don’t have much unoccupied space in your home to carry out this practice, then go into a room, close the door and practice watching your back swing and forward swing in a full length mirror mounted on the wall in front of you.  Be sure to give yourself plenty of room behind and plenty of room in front towards the mirror, so your 2 and ½ pounds horseshoe does not do any damage to anything.)  You will be able to observe if you can swing a horseshoe straight or if you are going to have to rely on luck to throw the shoe straight at the stake when summer rolls around.

MARKING YOUR SHOE’S CENTER OF GRAVITY
24  To really make all of this clear and visible, the pitcher should take one of the favorite horseshoes pitched outside in the fair weather and find the center of gravity of the horseshoe, using the method described earlier in this writing.  Now mark a black dot in this center . . . (wait, there is a problem with this, the center of the shoe is not on the metal of the shoe, but rather in between the blades somewhere).  So, take something like a rubber band, or even better a strip of clear Scotch tape, and stretch it along this line between the blades that designates the center line dividing the weight of the left half of the shoe with the right half of the shoe.  Now, cut out a half inch diameter black dot and tape it in the center of this rubber band or use a black marker to make this half inch diameter black dot on the clear tape (hint, it should be exactly halfway on the rubber band or tape if the pitcher’s favorite shoes are balanced).

PITCHING HORSESHOES IN SLOW MOTION
25  This is where all the fun begins and the pitcher finds out in slow motion why the ringers just weren’t coming for some mysterious reason this past summer.  First, the pitcher should stand where normally standing outside in relation to the stake and pit at the pitcher’s end of the stretched rope.  The rope should have been stretched across the path where the pitcher swings forward before delivering the shoe to the other end.  (note:  do not release the horseshoe during these slow practice swings in the house unless the pitcher had 40 feet of hallway and all the necessary work was completed to put in indoor pits).  Take a few slow practice swings with the turn used last during the summer months.  Look down at the line and note that the center of gravity of the shoe rarely follows the rope during the application of the turn motion on the horseshoe.  That is why the pitcher was not throwing consistently this past summer when pitching outside.  Unless consciously aware of the importance of creating all the turn rotation motion of the horseshoe around the center of gravity of the shoe, most pitchers are just getting lucky sometimes when they are pitching outdoors and swinging their hand straight along this line to the stake or rotating their shoe around the pivot point of the center of the shoe.  Keep practicing this delivery in slow motion over and over.  Be sure to hang onto the shoe while indoors.  And don’t be too anxious to speed up the swing to normal speed.  If this swing and turn rotation on the horseshoe cannot be mastered in slow motion, then you might as well get out the chessboard, because your horseshoe pitching game is not going to improve.  Just kidding, you may continue to throw horseshoes outside as long as you are content with luck.  At least, you will understand from these indoor practices, why the shoe is not heading for the other stake and turning properly around the center of gravity of the shoe.  (Later on in this writing, an easier way will be explained for how to lay this rope or wire toward where the stake would be if you had 40 feet of space in your home.  The method has to do with the amount of distance in feet for every inch the rope or wire goes towards the true stake to stake straight line.)  Also, the pitcher may also wish to create that line on the wall that shows the point where the center of gravity of shoe is when at the side and where it is at the end of the forward swing where it would be released.  Use masking tape rather than marking the wall up with a black marker.

PITCHING HORSESHOES IN THE SNOW
26  Once this slow motion forward swing is mastered. . . the pitcher can observe that the center of the shoe is going down the center of the rope toward the other stake and all the time the pitcher is applying the turn rotation motion on the shoe, the center of the shoe is still following the path of the rope, then the pitcher might feel confident enough to start speeding up the swing, until at last the pitcher can confidently swing at full speed and execute the forward swing and turning of the shoe right on top of the rope.  At this point, even in the winter, the pitcher will be tempted to go out to the outdoor courts, covered with six to eight inches of snow and let a couple rip.  Warning:  the first few shoes thrown will be easy to find, because there will be clear imprints in the snow where the shoes hit.  But after a while, the pitcher will not know which imprints are new ones, indicating where the latest two pitches landed.  Of course, if everything in this article was mastered by the pitcher, there will only be imprints around the stake.  Additional Warning:  the low temperature outdoors will likely alter your pitching ability.  So it would still be advisable to wait for spring.

PITCHING HORSESHOES WITH A TRAINING ROPE
27  When spring rolls around, the pitcher is going to want to take the indoor rope along when starting to pitch again on the outdoor courts.  The pitcher will think of the rope as training wheels.  Tying the rope to the opposite stake and stretching toward the other stake and running on the ground along the pitcher’s full swing.  The pitcher might even employ a fellow pitcher to stand behind the pitcher and tighten up the rope when the swing is executed in slow motion.  If the two of them get real creative, they may even design an adjustable stand up post that can be placed somewhere near the middle of the court that goes up as high as eight feet, so that the rope can be stretched up over the top of the post.  If it has a little slack as it drops in to where the pitcher is swinging and then tied down behind the pitcher, then we have a real nice set of training wheels indeed.  If the pitcher puts the correct turn on the shoe, throws it with the correct force at the right distance and stays over the imaginary line (actually a physical training rope), then the pitcher may begin pitching nearly 100% ringers before the following summer is over.  Oh well, one can dream can’t one?  Later on, I guess we should talk about knowing all there is about the physics and mathematics of pitching ringers, but not being able to avoid the human trait of choking.  Choking brings the ringer percentage down, down, down.

THE MATHEMATICS OF THE ALIGNMENT AND WHERE TO STAND TO TAKE ADVANTAGE
28  If you got this far in the reading, you are in for the biggest inside secret of horseshoe pitching.  I will now explain the “mathematics of the alignment”.  I once read where a pitcher asked the question if a pitcher could legally pitch the horseshoe while standing in the pit?  The pitcher’s thinking was surely that if the back swing and the forward swing could simply be down the straight line between the two stakes (I believe a 15 inches stake sticking up out of the ground would interfere with the swinging horseshoe if a short horseshoe pitcher pitched down the straight line between the two stakes) then the alignment of the pitch would be so much easier to control.  Well, other than that obstacle of the 15 inches stake and the sticky watered down clay that the pitcher would be standing in, it would seem like getting the proper alignment would be easier if the pitcher could stand in the pit.  With the application of mathematics, the alignment of the swing of the horseshoe is almost as simple to figure out as throwing from stake to stake.  The center of most horseshoe stakes is 18 inches away from the edge of the cement walkway that the pitcher pitches on.  Simply add on 2 more inches and the pitcher has a point that is exactly 20 inches from the center of the stake.  Why 20 inches?  That is where the mathematics comes into the calculation on where to stand and where to greet the stake and where to execute the back swing and where to execute the all-important forward swing.  From the center of one stake to the other is exactly 40 feet if pitching on a regulation court.  With 12 inches in each foot, the stakes are exactly 480 inches apart.  Why do we convert feet to inches?  We are coming to that.

USING A NICE 3 FEET STEP TO THE FOUL LINE FROM THE SPOT
30A  While standing in the spot to make all our calculations work out with one inch gained on the stake lines for every 2 feet the shoe travels during the forward swing past our leg and up to our forward foot after taking our near 3 feet step, the shoe should now be 1-1/2 inches closer to the stake line (2 feet gains 1 inch, so 3 feet gains 1-1/2 inch).  What does this all mean?  It simply means this.  A scope on a rifle allows the shooter to put the cross hairs at one end of the scope with the eyeball at the other end of the scope centered on the cross hairs, right on the target before pulling the trigger, giving the shooter a much better chance of hitting the target than if the shooter just raised up the rifle and fired in the vicinity of the target.  The horseshoe pitcher now has a scope, so to speak.  While facing straight down the court, from the bottom of the pitcher’s forward swing, the pitcher’s shoe must be 1 and ½ inches closer to the stake line when it passes the point that is about 3 feet from where the back leg is standing, or not coincidentally at the foul line.  Remember the center of the shoe started out at the bottom of the forward swing by the leg exactly over the spot that was 20 inches from the center of the stake.  So after traveling 3 feet, it should be 1-1/2 inches closer to the stake line or ½ inch from the edge of the pit.  Who says horseshoe pitching is not a game of inches.

THREE DIFFERENT WAYS TO ORIENT THE BODY WITH THE STEP AND SWING
30B  Now I began the last paragraph stating that the pitcher is facing straight down the court.  This would require that the forward swing begin going out from the body by 1-1/2 inches by the time it has traveled 3 feet in the pitcher’s hand from the leg up.  In order to keep a straight swing, the pitcher must slightly turn toward the stake so that a straight swing passes along this alignment path.  Both of these methods of delivery require that the stepping foot step straight ahead.  Another method some pitchers use (probably without thinking this deeply into it) is to look straight ahead while stepping slightly across their stationed foot by about 1-1/2 inches toward the stake and slightly twisting their body to make up the 1-1/2 inches.  Since right handed pitchers generally miss to the right and left handed pitchers generally miss to the left, it would seem that most pitchers overestimate this minor angle 1-1/2 inches adjustment in their swing toward the stake.  It looks like so much when they look all the way down the court and see the big 20 inches difference, but taking care of only 1-1/2 inches in 3 feet at their end (using their 3 feet scope swing) will take care of the 20 inches at the other end!  (Remember, for consistent illustration purposes only, I have used 20 inches from the stake for the swing line beside the leg.  If the pitcher stands at the edge of the pit with the side of the shoe and the hand hanging down with the center of the shoe over a point in the pit that is 10 inches from the center of stake, then 10 inches will have to be made up in 40 feet of flight or 1 inch per 4 feet.  This would be the same for a 15 inches point in the pit (or 3 inches toward the stake from the edge of the pit, in which case the rate to make up would be 15 inches in 40 feet of distance or 1 inch per 2 and 2/3 feet.)

SEEING IS BELIEVING
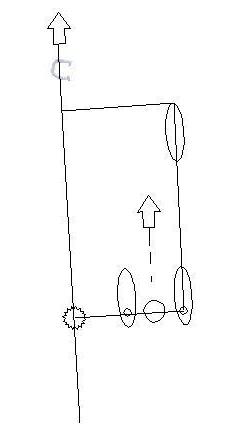
30C  The illustration to the right shows an aerial view of where the right-handed pitcher might stand and step if an attempt is made to swing the the horseshoe square with the shoulders and aligned perfectly with the stake.  (Scroll on down to see the  illustration for the left-handed pitcher).  In order to use measurements in our discussion, let's say the pitcher swings the shoe approximately 6 inches away from the center of the right foot and approximately 12 inches away from the center of the left foot.  This would make the center of the left foot exactly 6 inches away from the center of the right foot.  (To visualize this possibility, simply stand with a 12 inches ruler placed on top of your feet with the end at the center of the left foot and the half way point of the ruler at the center of the right foot, and note that the other end of the ruler is approximately where a pitcher might swing the shoe).  We are not saying here that these are the ideal distances for the feet to be apart and the distance from the leg to swing the shoe.  WHATEVER WORKS FOR EACH PITCHER SHOULD BE USED FOR THAT PITCHER!  We are just setting up some measurements to follow our idea on the step toward the other stake.  Now looking at the illustration, the pitching arm needs to swing straight at the opposite stake, if there is to be any chance for the horseshoe to go on as a ringer.  But the illustration shows the importance of the step forward with the stepping foot.  If the arm swings straight toward the stake, the foot steps straight forward from its beginning position (with the line between the two feet representing the "square" shoulder), thus ending the step the same distance from the plane of the swinging horseshoe as it was from it when the horseshoe was beside the leg (tilting the head to the left or right during the forward step is a bad habit for pitchers who do not compensate for this movement with the rest of their delivery).  The head should also go straight forward in order to keep the shoulder from breaking out of the perpendicular relationship with the stepping foot and the swinging horseshoe.  In this system of delivery, the slightest turning of the shoulder will begin to affect the straight aligned swing toward the stake.  Again, to be emphasized here, this is the illustration of a form or system of delivery that is "square with the world".  The truth is that many or maybe even most horseshoe pitchers violate some part of this illustration and then compensate somewhere in their delivery for the violation.  If that is the way they pitch, it actually would not be totally fair to call it a violation as such, but in comparison to this "square" system of delivery, it is.

Some may cross over with the stepping foot in front of the stable foot, but then compensate their swing to make up for this movement.  I suspect, most good pitchers will tell the novice to be sure and place the bulk of the pitcher's body weight on the stable foot throughout the delivery until that moment when the weight shifts to the stepping foot.  This allows the balance to be maintained throughout the entire delivery process.  A smooth step in the timing is what helps keep the horseshoe on its original course.  A sudden drop onto the stepping foot is very likely to jar the shoe from its straight path to the stake and throw the shoe to the left or right of the stake.  Even with the "square" delivery, there is room for variation amongst pitchers.  Some will tell you it is easier for them to stand straight throughout the step forward.  Others will say it is more natural to bend forward and lean into your step.  Each pitcher should experiment with what is most comfortable with them.  Other variations are that some pitchers will use more of a "set" delivery method, by holding the shoe up close to their face and then swing back and forward and then let it fly.  Others will use what Dan Kuchcinski and others refer to as the "rhythm" delivery.  That is, they might begin by holding the shoe out in front of them, but then they swing the shoe back and forth (sometimes the other arm swings right along with the pitching arm) until it feels right to let it go; or they may have a delivery where they swing back and forth a given number of times (say 3) and then delivery it.  Again, the best advice is to not be afraid to experiment with each method to see which one is the most comfortable with each pitcher.  Studying the illustration above (or to the left for lefties), one can see that any pitcher who tells you to point your feet directly at the stake at the opposite end, if that is precisely what they do; must swing their arm not quite exactly square with their shoulder, else they would throw 6 inches or so to the right of the stake (for a right-hander) or 6 inches or so to the left of the stake (for a left-hander).  (Or whatever measurement the swinging shoe is from the center of the planted foot).  If one is actually trying to use the "square" delivery, where the shoulders always maintain that square with the swinging arm, then the planted foot would actually point about 6 inches or so to the left of the stake (if a string was run down the court from the middle of the planted foot).  Again, it must be emphasized here that whatever works should be used for each pitcher, but in order to discuss one such method, parameters must be set and adhered to in order to stay within that system!  I have seen videos of world champion pitchers who lean slightly over toward the swinging arm and it sure works for them.  The key is that whatever each great pitcher does, they consistently do it nearly 80% to 85% of the time.  Awareness of what one is actually doing is the first step to developing one's own timing and rhythm.  And it is this same awareness that allows good pitchers to make immediate corrections when they miss the stake.  The discussion here was intended for explaining one such delivery system to show what is being worked out by the great pitchers.  The rest of us just step up there and swing one way and step another way and release at different points and do all of this at various speeds and expect the same results pitch after pitch.  When we do this "consistently", we do get the same results, we miss repeatedly.  IT JUST DOESN'T WORK THAT WAY IF ONE IS TO BECOME A GOOD CONSISTENT PITCHER WHO HITS A HIGH PERCENTAGE OF RINGERS!  I've seen world champion pitchers look down first at their feet in relation to the pit beside them to assure themselves that they are starting everything correctly before they ever look down at the opposite peg.  I get the impression that they could probably put on a blindfold at this point and out pitch the rest of us.  Because their "form" takes over once they are positioned right in the beginning.  Form merely being that thing which they are able to do over and over again without breaking out of it.

30D  FINAL ADVICE WITH ONE'S CHOSEN FORM

THEORY IN PRACTICE WITH THE TRAINING ROPE
31  If a pitcher is serious to see this theory in practice (the discussion in 30B above, before the tangent discussion of 30C was inserted), just get out the old training rope and run it from the opposite stake to within ½ inch of the edge of the pit at the foul line and on through the back swing line and practice swinging down the alignment line until this 1-1/2 inches in a 3 feet swing can be down pretty consistently without the training rope.  The main point of the training rope is to help the pitcher visualize what needs to take place on the swing to keep the center of the shoe on the alignment, thus allowing the muscles and the mind to "remember" this minor adjustment in orientation to the pit and stake and foul line by the pitcher.

THE MATHEMATICS OF THE CROSSFIRE HORSESHOE PITCHER
32  The right handed pitcher who pitches from the right side of the stake and the left handed pitcher who pitches from the left side of the stake is called a crossfire pitcher.  The crossfire pitcher is pitching an additional 20 more inches away from the side of the stake at the pitching end which calculates out to be 40 feet and 1-5/8 inches from the stake being pitched at; or only 1-1/4 inches farther than the other pitchers have to pitch.  The only disadvantage I can see with the crossfire pitchers is they may have to eat an extra bowl of cereal in the morning of a big tournament to get up the extra energy to pitch the additional 1-1/4 inches, but other than that, there is no other major disadvantage as far as alignment goes.  But the major difference is that the cross fire pitcher has 40 inches to close in on the stake to stake line as opposed to 20 inches make-up on the other side.  40 inches at a distance of approximately 40 feet (or 41 feet and 5/8 of an inch) means the cross fire pitcher will cross about 3 inches toward the stake at a rate of make-up of 1 inch per 1 foot.  (In #14 above, we mention the fact that a shoe thrown a little higher with more arch will travel a little farther distance in the air than our illustrations of using a straight line on the ground--but we would need more information and calculus to start splitting inches here, so we continue to illustrate these principles using 40 feet, 20 inches and 40 inches.)  (note:  With the design of the open end of the shoe being 3-1/2 inches, calculating to hit dead center on a 1 inch stake gives the pitcher 1-1/4 inches on either side to hit the opening of the shoe onto the stake, plus the width of a shoe can be 7-1/4 inches, so less the 1 inch stake gives 3-1/8 inches on either side to still have a chance of going on depending on the angle of the spin and the slant of the points and hooks).  With the cross fire pitcher, the shoe can be released more in front of the body of the pitcher if the pitcher is facing straight ahead during the delivery of the shoe (see #30 above for different methods of facing during the delivery of the shoe and apply to the cross fire pitcher--straight facing down court with 3 inches cross toward the body, straight facing the stake with a straight swing, or straight facing down court with a twist of the body and a straight swing).  More could be said here, like some cross fire pitchers who face straight down the court and cross their body to make up the 3 inches per 3 feet may have a back swing that also swings out away from their body approximately 3 inches.  Whereas some pitchers pitching on the "normal" side using the facing straight ahead method of standing would swing approximately 1-1/2 inches behind them towards their body, so that they swing their arm straight ahead and slightly towards the stake to make up the 1-1/2 inches per 3 feet towards the stake to stake line.  If standing in the right spot by facing the distant stake, either the normal or cross fire pitcher can use a straight back swing and a straight forward swing and not worry about gaining on the stake to stake line, then the correctly orientated stand will take care of all of this.  This discussion is about showing that the 20 inches, 15 inches, 10 inches or whatever amount of inches off the stake to stake line is taken care of with only an inch or two during the swing in relation to the stake to stake line.  Now we are beginning to understand why so many different pitchers with all the various turns, stands, swings, methods of pitching, etc. make the game of horseshoe pitching so colorful.

33  OTHER PRINCIPLES TO BE DISCUSSED
CONCLUSION
READERS’ RESPONSES AND COMMENTS